Abstract
기존 통계기반 기계 번역과 다르게, 신경망 기계 번역은 성능을 극대화할 수 있게 함께 조정될 수 있는 단일 신경망 구축을 목표로 합니다.
최근에 제안된 모델은 encoder-decoder 계열로 decoder가 번역을 생성할 때 사용할 수 있는 고정 길이 벡터를 encode에서 만들어냅니다.
논문에서는 이러한 고정 길이 벡터가 기본적인 encoder-decoder모델의 성능 향상을 저하한다고 추측했고, 그에 따라 모델이 자동적으로 source sentence에서 예측할 단어와 관련 있는 부분을 찾을 수 있게 하는 방법을 제안합니다.
Introduction
전통적인 phrase-based 번역 시스템은 개별로 조정되는 많은 sub-components를 갖고 있었던 것과 다르게 신경망 기계 번역은 커다란 하나의 신경망 모델을 만드는 것을 시도했습니다.
이렇게 만들어진 대부분의 신경망 기계 번역 모델은 encoder-decoder계열에 속합니다. encoder 신경망은 source sentence를 읽고 고정된 길이의 벡터로 encode 합니다. 그런 다음 decoder신경망이 encoded vector로부터 번역을 출력합니다. 이러한 전체 시스템은 동시에 훈련됩니다.
위와 같은 모델이 가지고 있는 문제점은 source sentence에서 필요한 모든 정보를 고정된 길이의 벡터로 압축시켜야 할 필요가 있다는 것입니다. 이러한 문제는 신경망이 긴 문장에 대해서 대처하기 힘들게 만듭니다. 특히나 훈련 corpus보다 긴 문장에서 문제가 더욱 커집니다.
이러한 문제를 다루기 위해, 논문에서는 align과 translate을 함께 학습할 수 있는 encoder-decoder모델을 소개합니다.
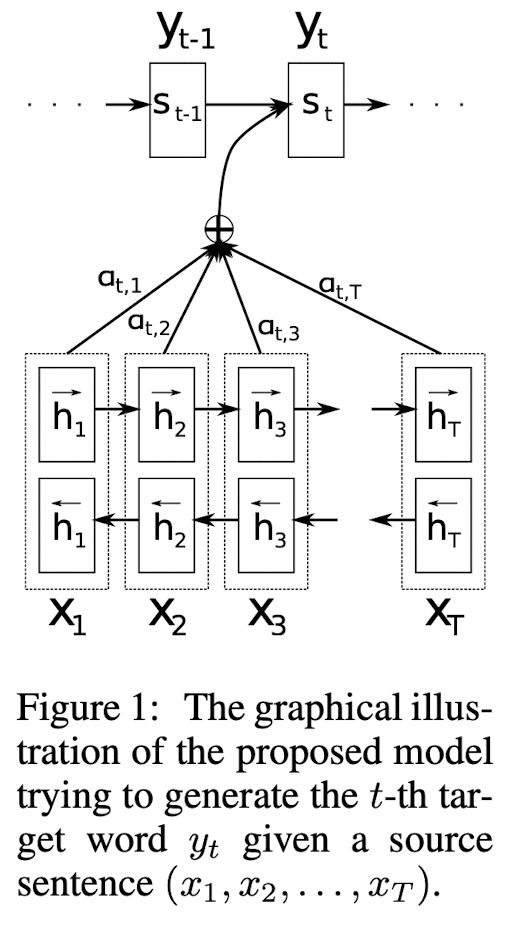
제안된 모델은 번역된 단어를 생성할 때마다 source sentence에서 관련된 정보가 가장 집중되어있는 위치 집합을 살펴보게 됩니다. 그 후 모델은 source positions와 이 전에 생성된 모든 target word를 이용해 조합된 context vector를 기반으로 target word를 예측합니다.
기본 encoder-decoder 모델과 이러한 접근법의 가장 큰 차이점은 전체 input sentence를 고정된 벡터로 encode하지 않는다는 것입니다. 대신에 input sentence를 sequence of vectors로 encode 하고 번역을 출력할 때 적절하게 이 vector의 부분집합을 선택하게 됩니다.
이 방법은 신경망 번역 모델이 source sentence의 모든 정보를 고정 길이 벡터로 변환하면서 찌그러트리는 것에 대한 문제에서 자유롭게 해 줍니다.
RNN Encoder-Decoder
먼저 RNN Encoder-Decoder라고 불리는 기본적인 framework에 대해 간단하게 설명하겠습니다.
Encoder-Decoder framework에서 encoder는 input sequence $\mathbf{x} = (x_1, \cdots, x_{T_x})$를 읽어서 vector $c$로 encoding 합니다.
$$h_t = f(x_t, h_{t-1})$$
$$c = q({h_1, \cdots, h_{T_x}})$$
- $h_t \in \mathbb{R}^n$ = 시간 $t$에 대한 hidden state
- $c$ = generated from the sequence of the hidden state
- $f$, $q$ = some nonlinear functions
decoder는 주어진 vector $c$와 이 전에 예측한 모든 단어들 ${y_1, \cdots, y_{t^\prime - 1}}$ 을 이용해서 다음 단어 $y_{t^\prime}$ 를 예측하도록 훈련됩니다.
$$p(\mathbf{y}) = \prod_{t=1}^T p(y_t | {y_1, \cdots, y_{t-1}}, c)$$
- $\mathbf{y} = (y_1, \cdots, y_{T_y})$
- $p(y_t | {y_1, \cdots, y_{t-1}}, c) = g(y_{t-1}, s_t, c)$
- $g$ = nonlinear function that outputs the probability of $y_t$
- $s_t$ = hidden state of RNN(decoder)
Learning to Align and Translate
Decoder
논문에서 제안한 새로운 모델에서는 위 식에 나오는 조건부 확률을 아래와 같이 정의하여 사용합니다.
$$p(y_i | y_1, \cdots, y_{i-1}, \mathbf{x}) = g(y_{i-1}, s_i, c_i)$$
여기서 $s_i$는 time $i$에 대한 디코더의 hidden state로 아래와 같이 계산됩니다.
$$s_i = f(s_{i-1}, y_{i-1}, c_i)$$
이 식에서 활성화 함수 $f$는 GRU를 사용했습니다.
$s_i$가 계산되는 과정을 좀 더 자세히 살펴보겠습니다.
$$s_t = f(s_{i-1}, y_{i-1}, c_i) = (1 - z_i) \circ s_{i-1} + z_i \circ \tilde{s_i}$$
- $\circ$ = element-wise multiplication
- $z_i$ = output of the update gate
- $\tilde{s_i}$ = update state
$$\tilde{s_i} = \tanh(We(y_{i-1}) + U[r_i \circ s_{i-1}] + Cc_i)$$
- $e(y_{i-1}) \in \mathbb{R}^m$ = m-dimensional embedding of $y_{i-1}$
- $r_i$ = output of reset gate
여기서 update gates $z_i$는 각 hidden unit이 이 전의 activation을 얼마나 유지할지를 정해주고, reset gates $r_i$는 이 전의 state로부터 어떤 정보를 얼마나 많이 reset 시킬 것인지를 결정합니다. 각각은 아래와 같이 계산됩니다.
$$z_i = \sigma(W_ze(y_{i-1}) + U_zs_{i-1} + C_zc_i)$$
$$r_i = \sigma(W_re(y_{i-1}) + U_rs_{i-1} + C_rc_i)$$
- $\sigma(\cdot)$ = logistic sigmoid function
decoder의 각 단계에서 앞에서 본 조건부 확률을 계산하게 됩니다.
그리고 이 식에서 특이한 점은 확률을 계산할 때 별개의 context vector $c_i$를 이용해서 계산을 하게 됩니다.
context vector $c_i$는 sequence of $annotations$ $(h_i, \cdots, h_{T_x})$를 이용하여 만들어집니다. 각 annotation $h_i$는 input sequence의 $i$번 째 단어를 둘러싼 부분에 초점을 맞춘 전체 입력 시퀀스에 대한 정보가 포함되어 있습니다.
context vector $c_i$는 이러한 $h_i$의 가중합(weighted sum)으로 구해집니다.
\begin{align}
c_i & =\sum_{j=1}^{T_x} \alpha_{ij}h_j\\
\alpha_{ij} & =\frac{\exp(e_{ij})}{\sum_{k=1}^{T_x} \exp(e_{ik})}\\
e_{ij}& ={v_a}^T \tanh(W_as_{i-1} + U_ah_j)
\end{align}
$h_j$는 source sentence에서의 $j$번 째 annotation입니다. 그리고 $v_a \in \mathbb{R}^{n^\prime}, W_a \in \mathbb{R}^{n^\prime \times n}, U_a \in \mathbb{R}^{n^\prime \times 2n}$은 가중치 행렬입니다.
위 식에서 $\alpha_{ij}$는 target word $y_i$가 source word $x_j$에 align 될 확률을 의미합니다.
Encoder
보통의 RNN에서는 input sequence $\mathbf{x}$를 $x_1, \cdots, x_{T_x}$순서로 읽어 들입니다.
하지만 논문에서 주어진 구조는 이 전의 단어뿐 아니라 다음에 오는 단어에 대한 정보도 요악하고 싶어서 BiRNN을 사용합니다.
먼저 모델이 단어장의 크기를 이용해 원-핫 벡터로 표현된 벡터의 sequence를 input으로 받아옵니다.
$$\mathbf{x} = (x_1, \cdots, x_{T_x}), x_i \in \mathbb{R}^{K_x}$$
그리고 forward state$(\overrightarrow{h_1}, \cdots, \overrightarrow{h_{T_x}})$를 계산해줍니다.
$$\overrightarrow{h_i} =\begin{cases}(1 - \overrightarrow{z_i}) \circ \overrightarrow{h}_{i-1} + \overrightarrow{z_i}\circ\overrightarrow{\underline{h}_i} & ,i > 0\\0 & ,i = 0\end{cases}$$
\begin{align}
\overrightarrow{\underline{h}_i} & =\tanh(\overrightarrow{W}\overline{E}x_i + \overrightarrow{U}[\overrightarrow{r}_i \circ \overrightarrow{h}_{i-1}])\\
\overrightarrow{z}_i & =\sigma(\overrightarrow{W}_z\overline{E}x_i + \overrightarrow{U}_z\overrightarrow{h}_{i-1})\\
\overrightarrow{r}_i& =\sigma(\overrightarrow{W}_r\overline{E}x_i + \overrightarrow{U}_r\overrightarrow{h}_{i-1})
\end{align}
$\overline{E} \in \mathbb{R}^{m\times K_x}$는 word embedding matrix입니다.
backward states$(\overleftarrow{h_1}, \cdots, \overleftarrow{h_{T_x}})$도 위와 비슷한 방법으로 계산해줍니다.
여기서 word embedding matrix $\overline{E}$는 forward와 backward RNN에 공유됩니다.
이렇게 구한 forward and backward hidden states를 concatenate 하여 $(h_1, \cdots, h_{T_x})$를 구해줍니다.
$$h_i = \begin{bmatrix}\overrightarrow{h_i} \\ \overleftarrow{h_i} \end{bmatrix}$$
이렇게 구한 $h_i$는 이 전의 단어와 다음에 따라 올 단어들에 대한 요약을 담고 있습니다. 그리고 이들은 나중에 decoder가 context vector를 계산할 때 사용됩니다.
Results
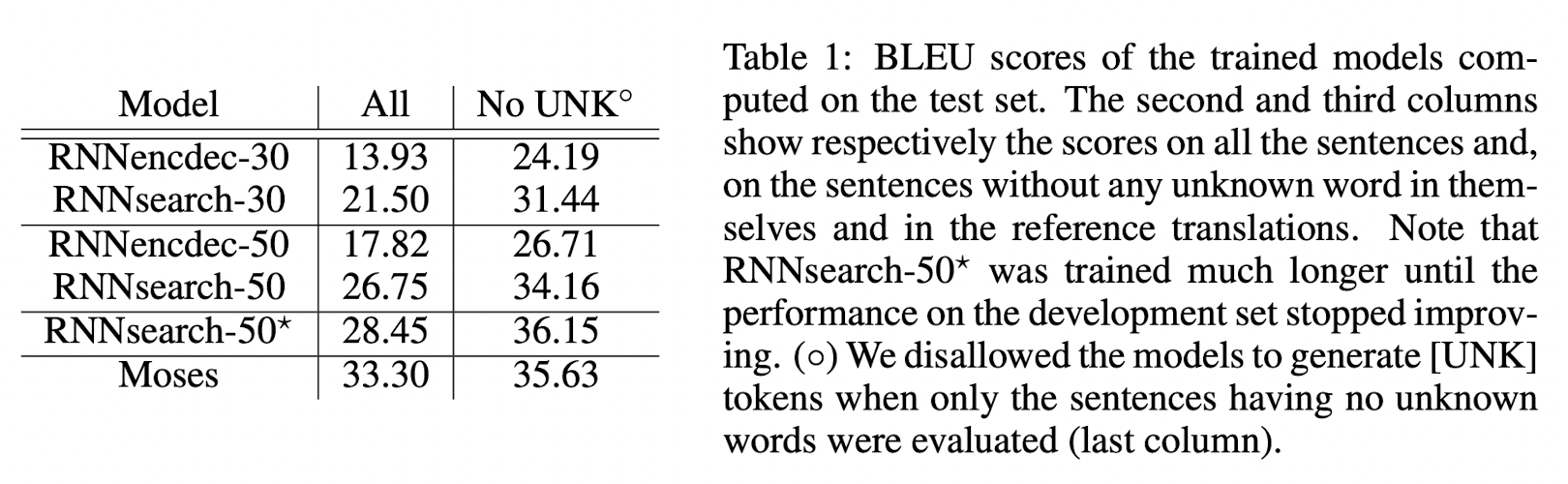
Table 1은 번역 성능을 비교한 것입니다.
여기서 RNNencdec는 이 전의 RNN Encoder-Decoder모델이고 RNNsearch는 논문에서 제안된 모델입니다. 뒤의 숫자는 훈련 과정에서의 sentence의 최대 길이를 나타낸 숫자입니다. (RNNencdec-30은 RNNencdec모델을 문장이 가지고 있는 단어의 개수가 최대 30개인 훈련 데이터로 학습시킨 모델)
결과를 보면 RNNsearch 모델의 성능이 더 좋은 것을 알 수 있습니다.
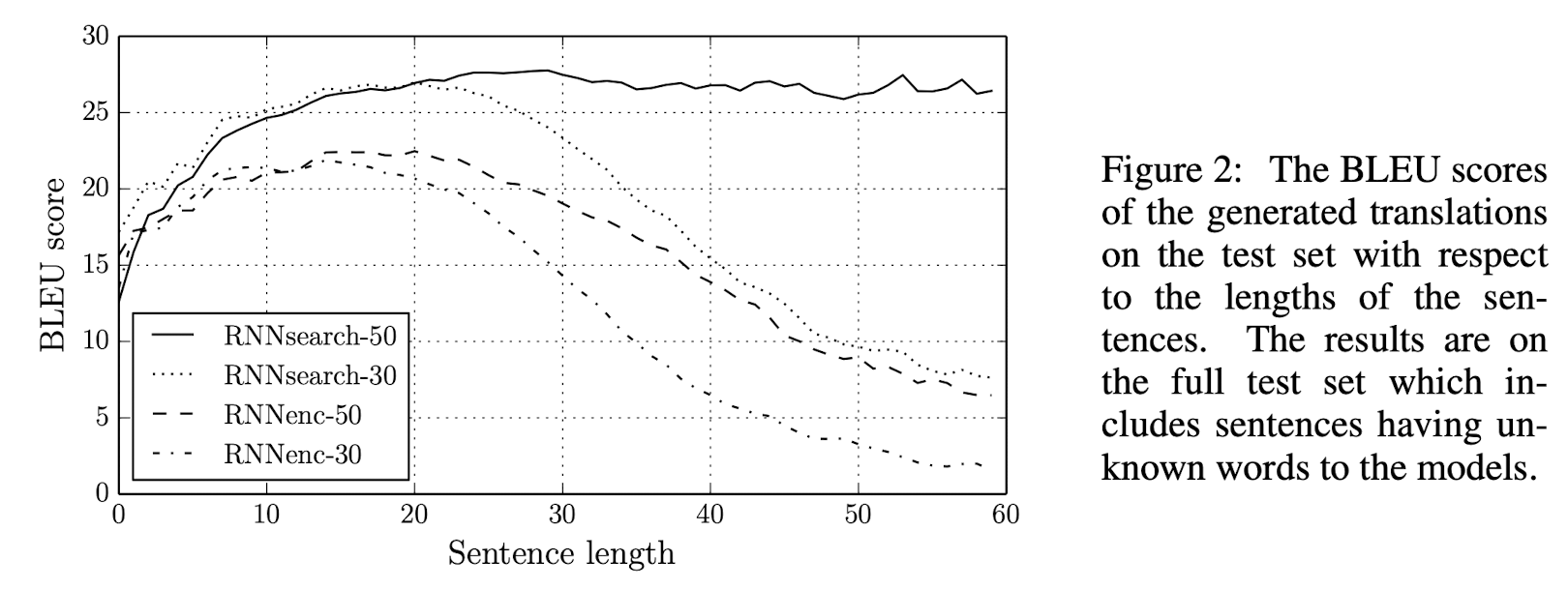
위 그래프는 처음에 논문에서 고정된 길이의 벡터로 바꾸는 방법은 문장이 길어질수록 성능이 낮아질 것이라는 주장을 뒷받침하는 결과입니다.
실제로 RNNencdec 모델은 문장의 길이가 증가할수록 급격하게 성능이 낮아지는 것을 볼 수 있습니다.
그에 반해 RNNsearch모델은 문장의 길이에 좀 더 robust 한 모습을 보입니다. 특히 RNNsearch-50 모델은 문장의 길이가 50을 넘어가더라도 성능이 저하되는 모습을 보이지 않습니다.
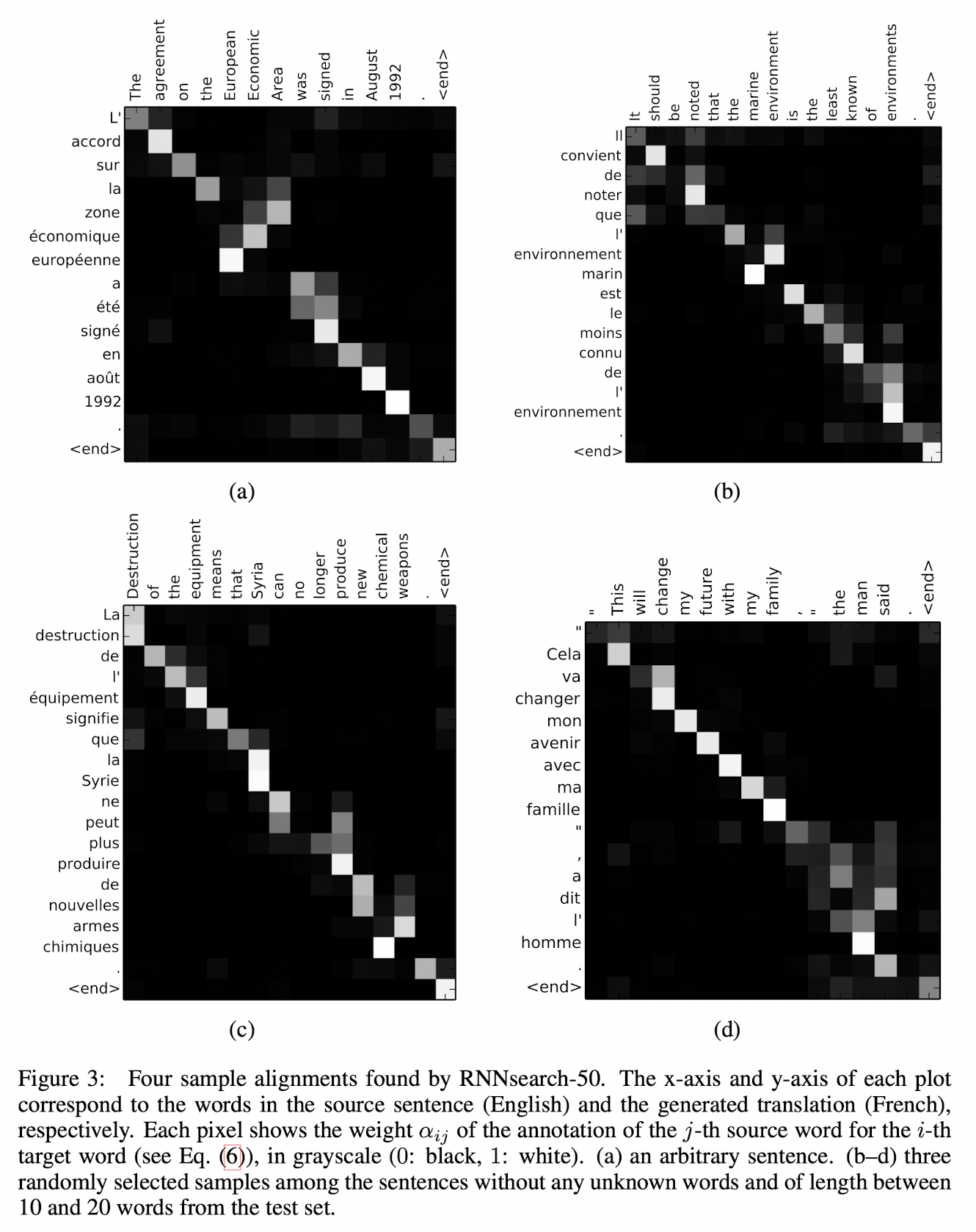
Figure 3은 annotation weights $\alpha_{ij}$를 시각화한 것입니다. 이를 통해 우리는 target word를 만들어낼 때 source sentence의 어느 부분을 중요하게 여겼는지 알 수 있습니다. 색이 어두울수록 가중치가 작은 것입니다.
Conclusion
논문에서는 기존의 방식에서 source sentence를 고정된 길이의 벡터로 변환하는 것이 긴 문장을 번역함에 있어서 문제를 일으킬 수 있다고 보았습니다.
이 때문에 모델이 target word를 만들 때 encoder에서 계산된 annotations를 찾거나 input words의 일정 부분을 찾는 방법을 제시했습니다. 이 방법은 모델이 전체 문장을 고정 길이 벡터로 encode 해야 하는 부담을 줄여주었고, target word를 만드는 것과 관련 있는 정보에만 집중할 수 있도록 해주었습니다.
이 방법을 적용한 모델이 실제로 문장의 길이에 상관없이 성능이 더 좋은 것을 보였습니다.



