이 게시물은 밑바닥부터 시작하는 딥러닝 1권을 바탕으로 작성되었습니다.
이번 장의 주제는 신경망 학습입니다. 여기서 학습이란 훈련 데이터로부터 가중치 매개변수의 최적 값을 자동으로 획득하는 것을 뜻합니다.
이번 장에서는 신경망이 학습할 수 있도록 해주는 지표인 손실 함수를 소개합니다. 이 손실 함수의 결괏값을 가장 작게 만드는 가중치 매개변수를 찾는 것이 학습의 목표입니다. 손실 함수의 값을 작게 만드는 기법으로 함수의 기울기를 활용하는 경사법도 소개합니다.
훈련 데이터와 시험 데이터
기계 학습에선 데이터를 훈련 데이터와 시험 데이터로 나눠 학습과 실험을 수행하게 됩니다. 훈련 데이터를 이용해 모델 훈련을 하고, 시험 데이터로 테스트를 보는 것입니다. 이렇게 하는 이유는 우리가 원하는 것은 새로운 데이터에 대해서도 성능이 잘 나오는 범용적인 모델을 만드는 것이기 때문입니다.
하지만 오버피팅 문제가 발생할 수 있는데, 훈련 데이터에 지나치게 최적화되는 경우를 오버피팅이라고 합니다.
손실 함수
모델이 훈련을 할 때 자기가 훈련을 잘하고 있는지에 대한 지표로 이용하는 것이 손실 함수입니다. 손실 함수는 훈련의 결과가 얼마나 안좋은지에 대한 척도이기 때문에 모델은 손실 함수를 최소화하는 방향으로 학습을 진행하게 됩니다. 사용할 수 있는 손실 함수로는 오차 제곱합과 교차 엔트로피 오차가 있습니다.
오차 제곱합
오차제곱합의 수식은 다음과 같습니다.
$$E = \frac{1}{2} \sum_k (y_k - t_k)^2 $$
여기서 $y_k$는 예측값, $t_k$는 정답 레이블입니다.
def sum_squares_error(y, t):
return 0.5 * np.sum((y-t)**2)교차 엔트로피 오차
교차 엔트로피 오차의 수식은 다음과 같습니다.
$$E = - \sum_k t_klog(y_k)$$
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))코드에서 delta를 더해준 이유는 log안의 값이 0이 되는 것을 방지하기 위함입니다.
미니배치 학습
지금까지는 데이터 하나를 넣었을 때 손실 함숫값을 구했습니다. 3장에서처럼 훈련을 배치 단위로 진행하게 된다면 배치 전체에 대한 평균 손실 함수를 구해야 합니다. 바뀐 수식은 아래와 같습니다.
$$E = - \frac{1}{N} \sum_n \sum_k t_{nk}log(y_{nk})$$
여기서 $t_{nk}$는 n번째 데이터의 k번째 값을 의미합니다.
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 원-핫 벡터이면 정답 레이블의 인덱스로 변경
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
수치 미분
미분
우리가 알고 있는 미분에 대한 수식은 다음과 같습니다.
$$\frac{df(x)}{d x} = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$$
하지만 우리가 코드로 구현할 때 h가 한없이 0에 가깝다는 것을 표현할 수가 없기 때문에(너무 작은 값에 대해서는 계산이 되질 않음) 중심 차분을 이용한 식으로 바꿔 줘야 합니다. 식은 아래와 같습니다.
$$\frac{df(x)}{d x} = \frac{f(x+h)-f(x-h)}{2h}$$
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)편미분
편미분이란 변수가 여러 개일 때 각 변수에 대한 미분입니다. 수식으로는 $\frac{\partial f}{\partial x_0}$, $\frac{\partial f}{\partial x_1}$ 처럼 씁니다.
신경망이 학습을 진행할 때 손실 함숫값이 최소가 되는 가중치 매개변수를 찾아가는 것이기 때문에 편미분을 통해 가중치의 각 원소가 변할 때 손실 함숫값의 변화량을 찾기 위해 편미분을 이용합니다.
기울기
$$∇𝑓(𝑥_1,𝑥_2,…,𝑥_𝑛)=(\frac{∂𝑓}{∂𝑥_1},\frac{∂𝑓}{∂𝑥_2},…,\frac{∂𝑓}{∂𝑥_𝑛})$$
이처럼 모든 변수의 편미분을 벡터로 정리한 것을 기울기(gradient)라고 합니다. 기울기는 다음과 같이 구현할 수 있습니다.
def numerical_gradient(f, x):
h = 1e-4
grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성
for idx in range(x.size):
tmp_val = x[idx]
#f(x+h) 계산
x[idx] = tmp_val + h
fxh1 = f(x)
#f(x-h) 계산
x[idx] = tmp_val-h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 값 복원
return grad경사법(경사 하강법)
경사 하강법은 손실 함수의 값을 점차 줄이는 방향으로 가중치를 갱신하며 손실 함수가 최소가 되는 지점을 찾아가는 방법을 말합니다.
수식으로 나타내면 다음과 같습니다.
$$x_0 = x_0 - \eta \frac{\partial f}{\partial x_0} \\
x_1 = x_1 - \eta \frac{\partial f}{\partial x_1}$$
위 식에서 $\eta$ 갱신하는 양을 나타냅니다. 이를 신경망 학습에서는 학습률(learning rate)라고 합니다.
학습률 값은 0.01이나 0.001등 미리 특정 값으로 정해 두어야 하는데 이렇게 미리 정해두어야 하는 파라미터를 하이퍼 파라미터라고 합니다.
경사 하강법은 다음과 같이 간단하게 구현할 수 있습니다.
def gradient_descent(f, init_x, lr=0.01, step_num=100):
x = init_x
for i in range(step_num):
grad = numerical_gradient(f, x)
x -= lr * grad
return x신경망에서의 기울기
가중치 매개변수에 대한 손실 함수의 기울기를 말합니다. 예를 들어 형상이 2X3 인 가중치가 $W$, 손실 함수가 L인 신경망을 생각해봅시다. 이 경우 기울기는 $\frac{\partial L}{\partial W}$로 나타낼 수 있습니다. 그러면 아래와 같은 모양이 됩니다.
$$W = \begin{pmatrix}
w_{11} & w_{12} & w_{13}\\
w_{21} & w_{22} & w_{23}
\end{pmatrix} \\
\frac{\partial L}{\partial W} = \begin{pmatrix}
\frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{13}} \\
\frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{23}}
\end{pmatrix}$$
2층 신경망 클래스 구현
앞서 배운 내용들을 종합하여 2층 신경망을 구현해보겠습니다.
import sys, os
sys.path.append(os.pardir)
from common.functions import *
from common.gradient import numerical_gradient
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
# 가중치 초기화
self.param = {}
self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def predict(self, x):
W1, W2 = self.params['W1'], self.params['W2']
b1, b2 = self.params['b1'], self.params['b2']
a1 = np.dot(x, W1) + b1
z1 = sigmoid(a1)
a2 = np.dot(z1, W2) + b2
y = softmax(a2)
return y
# x : 입력 데이터, t : 정답 레이블
def loss(self, x, t):
y = self.predict(x)
return cross_entropy_error(y,t)
def accuracy(self, x, t):
y = self.predict(x)
y = np.argmax(y, axis=1)
t = np.argmax(t, axis=1)
accuracy = np.sum(y==t) / float(x.shape[0])
return accuracy
# x : 입력 데이터, t : 정답 레이블
def numerical_gradient(self, x, t):
loss_W = lambda W : self.loss(x, t)
grads = {}
grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
grads['b2'] = numerical_gradient(loss_W, self.params['b2'])
return grads미니배치 학습 구현
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
(X_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
train_loss_list=[]
# 하이퍼 파라미터
iters_num = 10000 # 반복 횟수
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
network = TweLayerNet(input_size=784, hidden_size=50, output_size=10)
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
grad = network.numerical_gradient(x_batch, t_batch)
# 매개변수 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)전체적인 학습의 과정은 60000개의 학습 데이터에서 먼저 100개의 데이터를 뽑아 미니배치 만들어줍니다. 미니배치에 대한 가중치를 갱신하고 다시 100개를 뽑아 미니배치를 만들고 학습을 진행합니다. 이 과정을 총 10000번 반복합니다.
10000번 반복하면서 1 반복마다 loss결과를 리스트에 저장한 뒤 그래프로 나타내면 아래와 같습니다.
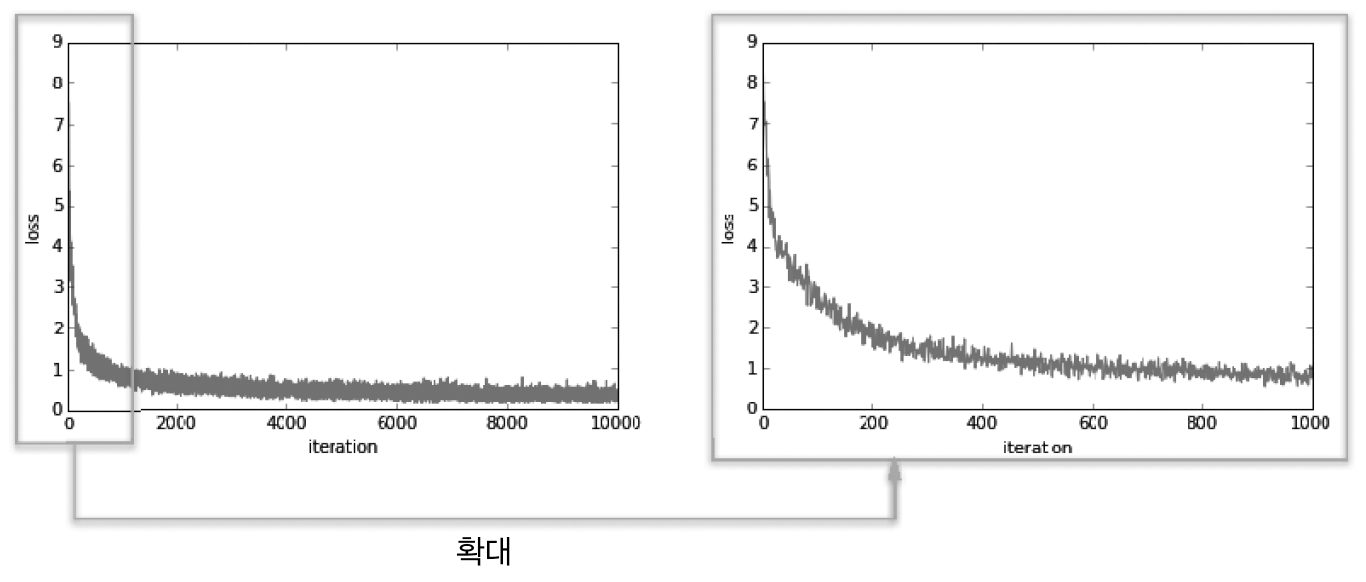
그래프를 보면 학습 횟수가 증가하면서 손실 함수의 값이 줄어드는 것을 볼 수 있습니다. 그래프를 통해 신경망이 학습을 잘하고 있는 것을 볼 수 있습니다.
시험 데이터로 평가하기
위 그림에서 보았듯이 신경망이 학습을 잘 진행했습니다. 하지만 훈련 데이터에 대한 학습만 했으므로 새로운 데이터가 들어왔을 때 성능이 좋은지는 알 수가 없습니다. 우리가 신경망을 학습하는 이유는 범용성을 키우기 위함이기 때문에 학습 데이터에 없는 데이터를 사용해 성능을 평가해봐야 합니다.
이번에는 학습 도중 정기적으로 훈련 데이터와 시험 데이터를 대상으로 정확도를 기록합니다. 1 에폭 별로 훈련 데이터와 시험 데이터에 대한 정확도를 기록합니다.
에폭(epoch)은 하나의 단위입니다. 1 에폭은 학습에서 훈련 데이터를 모두 소진했을 때의 횟수에 해당합니다. 지금의 예에서는 훈련 데이터가 60000개고 미니 배치 100개로 훈련을 진행하기 때문에 600번의 확률적 경사 하강법을 진행하면 모든 훈련 데이터에 대해 1번 경사 하강법을 진행한 것입니다. 이게 1 에폭입니다.
여기서 iters_num과 에폭이 헷갈릴 수 있는데 iters_num 은 우리가 설정한 미니배치에 대해서 확률적 경사 하강법을 진행하는 횟수에 대한 것입니다. 따라서 600번의 반복(iteration)을 진행했을 때가 1 에폭이 되는 것입니다.
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet
(X_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
train_loss_list=[]
train_acc_list = []
test_acc_list = []
# 1에폭당 반복 수
iter_per_epoch = max(train_size / batch_size, 1)
# 하이퍼 파라미터
iters_num = 10000 # 반복 횟수
train_size = x_train.shape[0]
batch_size = 100 # 미니배치 크기
learning_rate = 0.1
network = TweLayerNet(input_size=784, hidden_size=50, output_size=10)
for i in range(iters_num):
# 미니배치 획득
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 기울기 계산
grad = network.numerical_gradient(x_batch, t_batch)
# 매개변수 갱신
for key in ('W1', 'b1', 'W2', 'b2'):
network.params[key] -= learning_rate * grad[key]
# 학습 경과 기록
loss = network.loss(x_batch, t_batch)
train_loss_list.append(loss)
# 1 에폭당 정확도 계산
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
test_acc = network.accuracy(x_test, t_test)
train_acc_list.append(train_acc)
test_acc_list.append(test_acc)
print("train acc, test acc : " + str(train_acc) + ", " + str(test_acc))
그래프를 보면 학습 데이터와 테스트 데이터 모두에서 정확도가 좋아지고 있습니다. 또 두 정확도가 거의 차이가 없음을 알 수 있습니다. 다시 말해 오버피팅이 일어나지 않았다고 볼 수 있습니다. 만약 오버피팅이 일어났다면 학습 정확도는 올라가지만 테스트 정확도는 감소하는 경향을 보이게 됩니다.
'AI > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| Chapter 7. 합성곱 신경망(CNN) (0) | 2022.09.16 |
|---|---|
| Chapter 5. 오차역전파법 (0) | 2022.09.16 |
| Chapter 3. 신경망 (0) | 2022.09.15 |
| Chapter 2. 퍼셉트론 (0) | 2022.09.15 |



