자연어를 기계가 처리할 수 있도록 전처리 과정에서 텍스트를 벡터로 변환하는 과정을 벡터화(Vectorization)라고 합니다.
지금까지 벡터화 방법으로 DTM, TF-IDF를 배웠습니다. 그리고 이와 비슷하지만 다른 원-핫 인코딩(one-hot encoding)이라는 방법이 있습니다.
- DTM(Document-Term Matrix) : 문서에서 단어의 등장 빈도만을 고려해 벡터화하는 방법
- TF-IDF(문서-역문서 빈도) : 불용어 같이 거의 모든 문서에서 등장하지만 딱히 의미가 있지 않은 단어가 있기 때문에 단어마다 중요 가중치를 다르게 주는 방법
- 원-핫 인코딩(one-hot encoding) : 가지고 있는 단어장을 기준으로 해당하는 단어의 인덱스에만 1이고 나머지는 0인 벡터
간단하게 원-핫 인코딩에 대한 예를 보겠습니다.
문서 1 : 강아지, 고양이, 강아지
문서 2 : 애교, 고양이
문서 3 : 컴퓨터, 노트북
위와 같은 문서가 있다고 가정하고 단어장을 만들면 단어장의 크기는 5입니다. 이제 단어장에 있는 각 단어에 정수를 부여하겠습니다.
보통은 빈도수가 높은 단어를 시작으로 부여해줍니다.
강아지 : 1번
고양이 : 2번
컴퓨터 : 3번
애교 : 4번
노트북 : 5번
이제 만들어진 단어장을 이용해서 각 단어를 벡터로 표현하겠습니다.
| 강아지 | 1 | 0 | 0 | 0 | 0 |
| 고양이 | 0 | 1 | 0 | 0 | 0 |
| 컴퓨터 | 0 | 0 | 1 | 0 | 0 |
| 애교 | 0 | 0 | 0 | 1 | 0 |
| 노트북 | 0 | 0 | 0 | 0 | 1 |
이렇게 각 단어의 고유 번호(인덱스)에 해당하는 값만 1을 가지고 나머지는 0을 가지는 벡터로 만드는 게 원-핫 인코딩입니다.
여기서 각 단어 벡터의 차원은 단어장의 크기가 될 것입니다.
하지만 DTM, TF-IDF, 원-핫 벡터는 단어장의 크기에 영향을 받는 희소 벡터(Sparse vector)라는 특징이자 단점이 있습니다.
희소 벡터에서는 차원의 저주(curse of dimensionality)라는 문제가 있습니다.
빅데이터: 큰 용량의 역습 – 차원의 저주 (Curse of dimensionality)
데이터에서 모델을 학습할 때 독립적 샘플이 많을수록 학습이 잘 되는 반면 차원이 커질 수록 학습이 어려워지고 더 많은 데이터를 필요로 합니다.
thesciencelife.com
이 것 말고도 원-핫 벡터에서는 단어 간 유사도를 구할 수 없다는 문제가 있습니다.
벡터 간 유사도를 구하는 방법으로는 대표적으로 내적(inner product)이 있습니다. 하지만 원-핫 벡터는 서로 직교하는 성질이 있어 내적 값이 0이 됩니다. 이는 결국 원-핫 벡터를 통해서 단어 간 유사도를 구할 수 없음을 의미합니다.
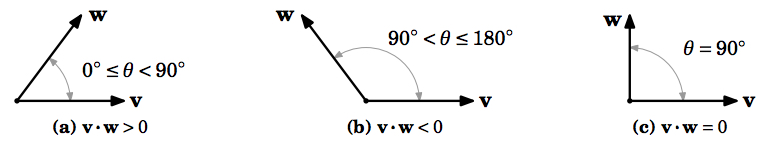
이에 대한 대안으로 기계가 단어장 크기보다 적은 차원의 밀집 벡터(Dense vector)를 학습하는 워드 임베딩(Word embedding)이 제안되었습니다. 이를 통해 얻는 밀집 벡터는 0과 1로만 이루어진 것이 아닌 다양한 실수값을 가지며, 이 밀집 벡터를 임베딩 벡터(Embedding vector)라고 합니다.
워드 임베딩(Word Embedding)
워드 임베딩에서도 단어를 벡터로 바꾸지만 벡터의 길이를 일정하게 정해줍니다. 일반적으로 벡터의 길이를 정해줄 때 단어장 크기보다 매우 작은 길이로 정해주기 때문에 각 벡터 값에 정보가 압축되어야 하고 결국 밀집 벡터(Dense vector)가 됩니다.

임베딩 방법마다 벡터의 값을 결정하는 다양한 방법이 있습니다.
아래의 표는 이해를 위해 임의로 단어를 임베딩 한 것입니다.
| 둥근 | 빨간 | 단맛 | 신맛 | |
| 사과 | 0.8 | 0.7 | 0.7 | 0.1 |
| 바나나 | 0.1 | 0.0 | 0.8 | 0.0 |
| 귤 | 0.7 | 0.5 | 0.6 | 0.5 |
만약 단어가 위와 같은 방법으로 임베딩 되었다면 그 의미는 아래와 같이 생각할 수 있을 것입니다.
- 0.8만큼 둥글고, 0.7만큼 빨갛고, 0.7만큼 달고, 0.1만큼 신 것은 사과다
- 0.1만큼 둥글고, 0.0만큼 빨갛고, 0.8만큼 달고, 0.0만큼 신 것은 바나나다
- 0.7만큼 둥글고, 0.5만큼 빨갛고, 0.6만큼 달고, 0.5만큼 신 것은 귤이다
결론적으로 워드 임베딩에서 중요한 것은 두 가지입니다.
- 한 단어를 길이가 비교적 짧은 밀집 벡터로 나타낸다.
- 이 밀집 벡터를 단어가 갖는 의미나 단어 간의 관계 등을 어떤 식으로든 내포하고 있다.
워드 임베딩은 2003년 Yoshua Bengio 교수가 NPLM(Neural Probabilistic Language Model)이란 모델을 통해 제안했습니다. 그 후 2013년 구글은 NPLM을 개선하여 정밀도와 속도를 향상한 Word2Vec을 제안했습니다. 이후로 FastText나 Glove 등과 같은 임베딩 방법이 추가로 제안되었습니다.
우선 Word2Vec에 대해 보겠습니다.
Word2Vec
1. 분포 가설(Distributional Hypothesis)
Word2Vec의 핵심 아이디어는 분포 가설을 따릅니다. 이는 비슷한 문맥에서 같이 등장하는 경향이 있는 단어들은 비슷한 의미를 가진다라는 내용의 가설입니다.
2. CBoW(Continuous Bag of Words)
CBow는 주변에 있는 단어들을 통해 중간에 있는 단어들을 예측하는 방법입니다.
- I like natural language processing
예를 들어 위와 같은 문장이 있다고 가정하겠습니다. CBoW는 중간에 있는 단어를 예측하는 방법이므로 {i, like, language, processing}으로부터 'natural'을 예측하는 것입니다. 이때 예측해야 하는 단어를 중심 단어(center word)라고 하고, 예측에 사용되는 단어들을 주변 단어(context word)라고 합니다.
중심 단어를 예측하기 위해 앞, 뒤로 몇 개의 단어를 살펴볼지 결정했다면 그 범위를 윈도우(window)라고 합니다.
윈도우의 크기를 정하고 나면, 윈도우를 계속 움직여서 주변 단어와 중심 단어를 바꿔가며 데이터를 만들 수 있는데, 이 방법을 슬라이딩 윈도우(sliding window)라고 합니다. 아래 그림은 윈도우 크기가 1일 때 슬라이딩 윈도우를 진행하는 과정을 나타낸 것입니다.

표로 정리해보면 아래와 같습니다.
| 중심 단어 | 주변 단어 |
| i | like |
| like | i, natural |
| natural | like, language |
| language | natural, processing |
| processing | language |
이렇게 만들어진 데이터셋에서 각 단어는 원-핫 벡터로 바뀌고, CBoW나 Skip-gram의 입력이 됩니다.
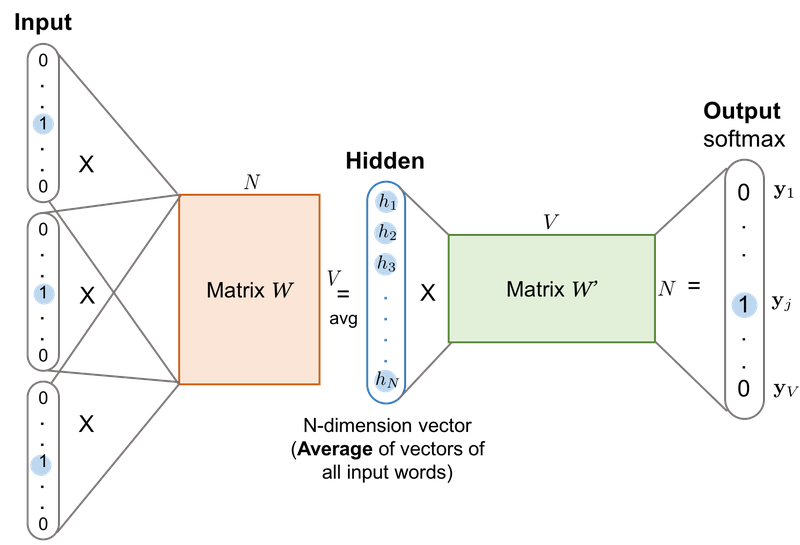
위 그림은 원-핫 벡터로 변환된 다수의 주변 단어를 이용해 원-핫 벡터로 변환된 중심 단어를 예측할 때의 CBoW의 동작 메커니즘을 보여줍니다.
그림에서 주황색 사각형이 첫 번째 가중치 행렬 $W$, 초록색 사각형이 두 번째 가중치 행렬 $W^\prime$입니다. 이 두 개의 가중치 행렬을 학습하는 것이 목적입니다.
CBoW 신경망 구조에서 주변 단어 각각의 원-핫 벡터는 입력층에 위치하고 중심 단어의 원-핫 벡터가 위치한 곳은 출력층이라고 볼 수 있습니다. CBoW에서 입력층과 출력층의 크기는 단어 집합의 크기인 $V$로 고정되어 있습니다. (원-핫 벡터로 표현되었기 때문) 하지만 은닉층의 크기는 하이퍼 파라미터로 사용자가 정해줘야 합니다.
우선 입력층에서 은닉층으로 가는 과정을 보겠습니다.
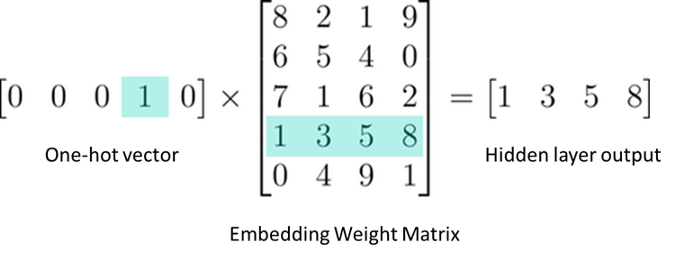
주변 단어로 선택된 각 벡터는 첫 번째 가중치 행렬($W$)과 곱해지게 됩니다. 이때 가중치 행렬의 크기는 $(V \times N)$입니다. 그런데 원-핫 벡터의 특성상 원-핫 벡터와 가중치 행렬과의 곱은 가중치 행렬의 $i$위치에 있는 행을 그대로 가져오는 것과 동일합니다.
이를 룩업 테이블(lookup table)이라고 합니다. 말 그대로 테이블에서 값을 그대로 lookup 해온다는 뜻입니다.
이제 이 룩업 테이블을 거쳐서 생긴 주변 단어 벡터들은 각각 $N$의 크기를 가집니다. CBoW에서는 이 벡터들을 모두 합하거나, 평균을 구한 값을 최종 은닉층의 결과로 합니다.

위 그림과 같은 계산을 통해 만들어진 은닉층의 결과도 각 $N$차원의 벡터가 될 것입니다. Word2Vec에서는 은닉층에서 활성화 함수나 편향을 더하는 연산을 하지 않습니다. 이렇게 단순한 행렬과의 곱셈만을 수행하기에 투사층(projection layer)라고도 부릅니다.
이제 은닉층에서 출력층으로 가는 과정을 보겠습니다.

은닉층에서 생성된 $N$차원의 벡터는 두 번째 가중치 행렬($W^\prime$)과 곱해집니다. 이 가중치 행렬($W^\prime$)의 크기는 $N \times V$이므로, 곱셈의 결과로 나오는 벡터의 차원은 $V$입니다. 출력층을 활성화 함수로 소프트맥스 함수를 사용하므로 이 $V$차원의 벡터는 모든 값의 합이 1이 되는 벡터로 변경됩니다.
CBoW는 이 출력층의 벡터를 중심 단어의 원-핫 벡터와의 손실(loss)을 최소화하도록 학습합니다. 이 과정에서 $W$와 $W^\prime$이 업데이트되는데, 학습이 완료되면 $N$차원의 크기를 갖는 $W$의 행이나 $W^\prime$의 열로부터 어떤 것을 임베딩 벡터로 사용할지를 결정하면 됩니다.
3. Skip-gram과 Negative Sampling
Skip-gram
Skip-gram은 CBoW와 다르게 중심 단어로부터 주변 단어를 예측합니다.

앞서 살펴본 그림입니다. CBoW의 경우 슬라이딩 윈도우 방식으로 얻을 수 있는 데이터는 5개였습니다. 하지만 Skip-gram은 데이터의 구성부터 다릅니다. 중심 단어로 주변 단어 각각을 예측하기 때문인데요. 아래 표와 같이 데이터를 구성하게 됩니다.
| 중심 단어 | 주변 단어 |
| i | like |
| like | i |
| like | natural |
| natural | like |
| natural | language |
| language | natural |
| language | processing |
| processing | language |
Skip-gram을 시각화한 그림은 다음과 같습니다.
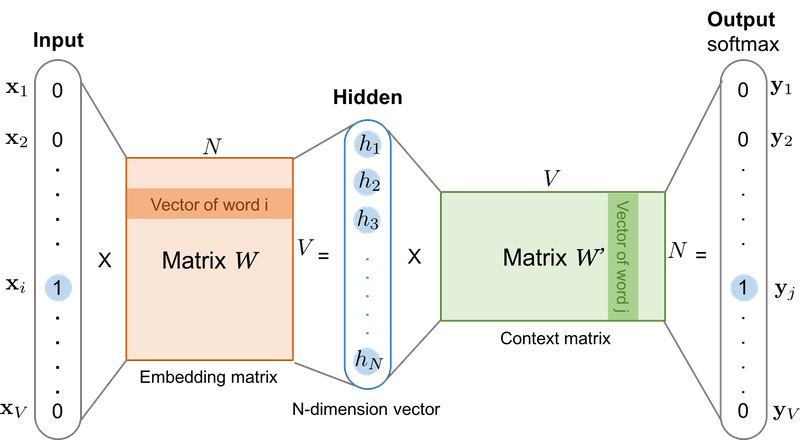
중심 단어로부터 주변 단어를 예측한다는 점, 그리고 이로 인해 중간에 은닉층에서 다수의 벡터의 덧셈과 평균을 구하는 과정이 없어졌다는 점만 제외하면 CBoW와 메커니즘 자체는 동일합니다.
네거티브 샘플링(Negative Sampling)
대체적으로 Word2Vec을 사용할 때는 SGNS(Skip-Gram with Negative Sampling)을 사용합니다.
그 이유는 기존의 Word2Vec구조는 연산량이 너무 많기 때문입니다.
Skip-gram의 학습 방법을 살펴보겠습니다. 모델의 구조는 단순해 보이지만 복잡한 과정을 거칩니다. 출력층에서 소프트맥스 함수를 통과한 $V$차원의 벡터와 레이블에 해당되는 $V$차원의 주변 단어의 원-핫 벡터와의 오차를 구하고, 역전파를 통해 모든 단어에 대한 임베딩 벡터를 조정합니다. 만약 단어장의 크기가 커지면 커질수록 이 작업은 너무 오래 걸리게 됩니다.
하지만 만약에 집중하고 있는 중심 단어와 주변 단어가 '롤', '배그'와 같이 게임와 관련된 단어라면, '김치찌개', 제육볶음'이라는 연관 관계가 없는 단어들의 임베딩 값을 굳이 업데이트할 필요가 없을 것입니다. 그래서 네거티브 샘플링은 소프트맥스 함수를 사용한 $V$개 중 1개를 고르는 다중 클래스 분류 문제를 시그모이드 함수를 이용한 이진 분류 문제로 바꿉니다.

기존의 skip-gram은 위 그림과 같습니다. 하지만 네거티브 샘플링을 사용하면 아래와 같이 바뀌게 됩니다.

좀 더 자세히 알아보겠습니다.
먼저 아래 예문으로 크기가 2인 윈도우를 슬라이딩하며 중심 단어, 주변 단어에 대한 데이터를 만들어줍니다.
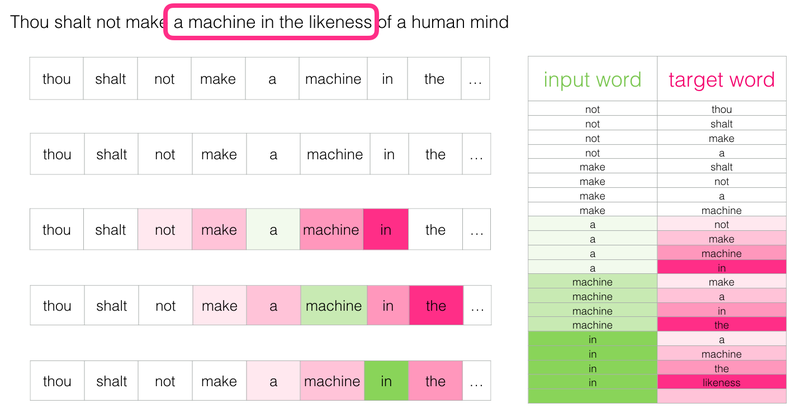
위의 중심 단어, 주변 단어에 해당하는 칼럼으로 이루어진 데이터에 새로운 레이블을 하나 달아줍니다. 우선 슬라이딩 윈도우를 통해서 만들어진 데이터셋에는 1이라는 레이블을 달아줍니다.

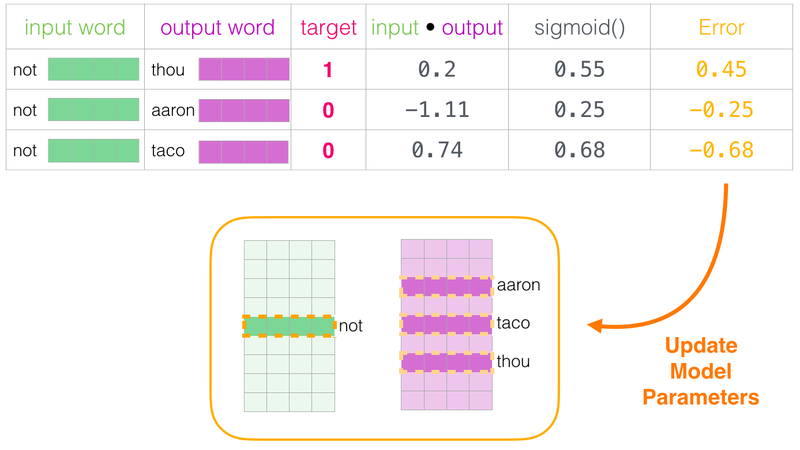
정상적으로 만들어진 데이터를 1로 레이블링 해주었으니 이제 실제로 이웃 관계가 아닌 단어의 경우를 데이터에 넣어주고 0으로 레이블링 해줍니다.
다시 말해 랜덤으로 단어장에 있는 아무 단어나 가져와 target word로 하는 데이터셋을 만들고 0으로 레이블링을 해주는 것입니다. 거짓(negative) 샘플을 만드는 방법이기 때문에 이를 네거티브 샘플링이라 부릅니다.

이렇게 만들어진 데이터셋으로 학습하면 Word2Vec은 더 이상 다중 클래스 분류 문제가 아니라 이진 분류 문제가 됩니다.
4. 영어 Word2Vec 실습과 OOV 문제
영어 Word2Vec 실습
실습은 google colab에서 진행했으며 훈련 데이터는 NLTK에서 제공하는 코퍼스를 이용했습니다.
먼저 NLTK에 내장된 코퍼스를 다운로드하고 corpus라는 변수에 저장하여 확인해줍니다.
# 코퍼스 다운로드
import nltk
nltk.download('abc')
nltk.download('punkt')
# 코퍼스 가져와서 corpus에 저장
from nltk.corpus import abc
corpus = abc.sents()
print('코퍼스의 크기 :' , len(corpus))
# output
코퍼스의 크기 : 29059이 코퍼스를 이용해 Word2Vec을 훈련시켜 보겠습니다.
from gensim.models import Word2Vec
model = Word2Vec(sentences = corpus, vector_size=100, window=5, min_count=5, workers= 4, sg=0)Word2Vec에서 사용되는 파라미터는 다음과 같습니다.
- vector_size : 학습 후 임베딩 벡터의 차원
- window : 컨텍스트 윈도우 크기
- min_count : 단어 최소 빈도수 제한(빈도가 적은 단어들은 학습 X)
- workers : 학습을 위한 프로세스 수
- sg : 0은 CBoW, 1은 Skip-gram
Word2Vec은 입력한 단어에 대해서 코사인 유사도가 가장 높은 단어를 출력하는 model.wv.most_similar를 지원합니다.
'man'과 가장 유사한 단어를 뽑아서 확인해보겠습니다.
similar_word = model.wv.most_similar('man')
print(similar_word)
이렇게 학습한 모델을 저장해 두고 필요할 때 가져와 사용하는 방법은 아래와 같습니다.
from gensim.models import KeyedVectors
model.wv.save_word2vec_format('.../w2v')
loaded_model = KeyedVectors.load_word2vec_format('.../w2v')# 가져온 모델을 이용해 유사한 단어 출력
similar_word = loaded_model.most_similar('man')
print(similar_word)
Word2Vec의 OOV문제
Word2Vec의 문제점 중 하나는 사전에 없는 단어에 대해서는 임베딩 벡터 값을 얻을 수 없다는 것입니다.
사전에 없는 단어는 평소에 우리가 잘 사용하지 않는 단어라 훈련 데이터에 들어있지 않은 단어이거나 혹은 오타가 발생했을 경우가 있습니다.
FastText
페이스북에서 개발한 FastText는 Word2Vec 이후에 등장한 워드 임베딩 방법으로, 메커니즘을 Word2Vec을 그대로 따르고 있지만, 문자 단위 n-gram(character-level n-gram) 표현을 학습한다는 점에서 다릅니다.
FastText는 단어 내부의 Subwords들을 학습한다는 아이디어를 가지고 있습니다.
n-gram에서 n은 단어를 분리할 때 문자 몇 개를 묶어서 분리하는지 결정하는 하이퍼 파라미터입니다. n을 3으로 잡은 tri-gram의 경우, 단어 'partial'은 아래와 같이 분리됩니다.
그리고 단어를 분리할 때 시작과 끝을 의미하는 '<' , '>'를 도입하여 내부 단어 토큰을 만들고, 여기에 추가적으로 기존 단어에 <와 >를 붙인 <partial> 토큰도 벡터화합니다.
# n = 3인 경우
partial -> <pa, par, art, rti, tia, ial, al>, <partial>그리고 실제로 사용할 때는 n을 값 하나로 지정하는 게 아니라 최댓값과 최솟값으로 범위를 지정할 수 있습니다.
# n = 2 ~ 3 인 경우
partial -> <p, pa, ar, rt, ti, ia, al, l>, <pa, par, art, rti, tia, ial, al>, <partial>그리고 이렇게 토큰화 된 내부 단어들 각각을 Word2Vec을 수행하여 벡터로 만들어주고, 최종적으로 벡터화된 내부 단어들의 벡터를 전 부 합하여 단어에 대한 벡터를 만듭니다.
FastText의 학습 방법은 Word2Vec과 크게 다르지 않습니다. 다만, 학습 과정에서 단어에 속한 문자 단위 n-gram 단어 벡터들을 모두 업데이트한다는 차이가 있습니다.
그리고 FastText는 Word2Vec과 달리 OOV와 오타에 강건하다(robust)는 특징이 있습니다. 이는 단어장에 없는 단어라도 해당 단어의 n-gram이 다른 단어에 존재하면 이로부터 벡터 값을 얻는다는 원기에 기인합니다.
한국어에서의 FastText
한국어도 FastText 방식으로 학습시킬 수 있습니다. 영어의 경우 알파벳 단위가 n-gram이었다면 한국어는 음절 단위로 나누거나 자소 단위로 나눌 수 있습니다.
- 음절 단위 FastText : (n = 3일 때) '텐서플로우' -> <텐서, 텐서플, 서플로, 플로우, 로우>, <텐서플로우>
- 자소 단위 FastText : (n = 3일 때) '국밥' -> <ㄱㅜ, ㄱㅜㄱ, ㅜㄱㅂ, ㄱㅂㅏ, ... >
여기서 자소 단위로 분리할 때 초성, 중성, 종성을 분리한다고 가정하고 만약 종성이 없는 경우 (예를 들어 '가') _라는 토큰을 대신 사용할 수 있습니다.
GloVe
글로브(Global Vectors for Word Representation, GloVe)는 2014년 미국 스탠포드 대학에서 개발한 워드 임베딩 방법입니다.
이 방법은 카운트 기반과 예측 기반 두 가지 방법을 모두 사용했다는 것이 특징입니다.
잠재 의미 분석(LSA, Latent Semantic Analysis)
잠재 의미 분석이란 DTM 등 입력 데이터에 특이값 분해를 수행해 데이터의 차원수를 줄여 계산 효율성을 키우는 한편 내재된(Latent) 의미를 이끌어내기 위한 방법론입니다.
대략적인 개념은 아래 그림과 같습니다.

$n$개의 문서를 $m$개의 단어로 표현된 입력 데이터 행렬 $A$가 주어졌다고 가정하겠습니다.
- 먼저 $A = U \Sigma V^T$형태의 Full SVD로 만들어줍니다.
- 이때 $A$의 0보다 큰 고윳값을 개수를 $r$이라 할 때 $k$($k < r$)를 사용자가 임의로 설정하고 $\Sigma_{k}$를 만듭니다.
- 이후 $U$와 $V$행렬에서 $\Sigma_k$에 대응하는 부분만 남겨 $U_k$, $V_k$를 만들어줍니다.
$$A_k = U_k \Sigma_k V_{k}^T$$
이런 방법으로 원래의 행렬 $A$를 $A_k$로 근사하여 표현할 수 있습니다.
LSA를 요약하면 DTM에 특이값 분해를 사용하여 잠재된 의미를 이끌어내는 방법론입니다.
하지만 이 방법은 몇 가지 한계가 있었습니다.
1. 차원 축소의 특성으로 인해 새로운 단어가 추가되면 다시 DTM을 만들어 새로 차원 축소를 진행해야 한다.
2. 단어 벡터 간 유사도를 계산하는 측면에서 Word2Vec보다 성능이 떨어진다.
반면, LSA와 대조되는 예측 기반의 방법은 Word2Vec과 같은 방법을 말합니다.
GloVe 연구진은 Word2Vec은 LSA보다 단어 벡터 간 유사도를 구하는 능력은 뛰어나지만, 코퍼스의 전체적인 통계 정보를 활용하지 못한다는 점을 지적했습니다. 그리고 카운트 기반과 예측 기반을 모두 사용한 임베딩 방법을 제안하였는데 그게 바로 GloVe입니다.
윈도우 기반 동시 등장 행렬(Window based Co-occurrence Matrix)
다음 3개의 문장이 있는 corpus가 있다고 가정하겠습니다.
- I like deep learning
- I like NLP
- I enjoy flying
이로부터 만들어진 동시 등장 행렬(Co-occurrence Matrix)은 다음과 같습니다.
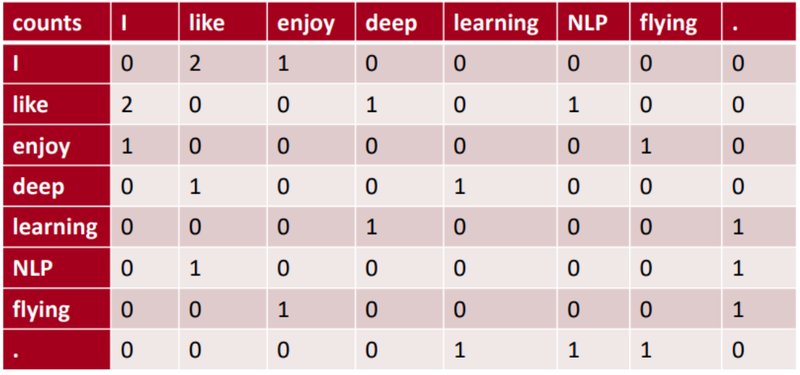
윈도우 기반 동시 등장 행렬은 행과 열을 전체 단어장의 단어들로 구성하고, 어떤 윈도우 크기(window size)에 대해서 i단어 주변에 k단어가 등장한 횟수를 i행 k열에 입력한 행렬입니다. 위는 경우는 윈도우 크기가 1입니다.
동시 등장 확률(Co-occurrence Probability)
동시 등장 확률 $P(k|i)$는 동시 등장 행렬로부터 특정 단어 i의 전체 등장 횟수를 카운트하고, 특정 단어 i가 등장했을 때 어떤 단어 k가 등장할 횟수를 카운트하여 계산한 조건부 확률입니다. 이때 i를 중심 단어(center word), k를 주변 단어(context word)라 합니다.
Glove는 동시 등장 행렬로부터 계산된 동시 등장 확률을 이용해 손실 함수를 설계합니다.
때문에 Glove는 동시 등장 행렬(카운트 기반)을 사용하고 있으면서 동시에 손실 함수를 통한 모델을 학습(예측 기반)시키는 방법론이라 볼 수 있습니다.
Glove의 아이디어를 한 줄로 요약하면 중심 단어 벡터와 주변 단어 벡터의 내적이 전체 코퍼스에서의 동시 등장 빈도의 로그 값이 되도록 만드는 것입니다.
GloVe의 손실 함수
우선 손실 함수를 설명하기 전에 각 용어에 대한 정리를 하겠습니다.
- $X$ : 동시 등장 행렬
- $X_{ij}$ : 중심 단어 i가 등장했을 때 윈도우 내 주변 단어 j가 등장하는 횟수
- $X_i$ : $\Sigma_j X_{ij}$ : 동시 등장 행렬에서 i행의 값을 모두 더한 값
- $P_{ik}$ : $P(k|i) = \frac{X_{ik}}{X_i}$ : 중심 단어 i가 등장했을 때 윈도우 내 주변 단어 k가 등장할 확률
- $\frac{P_{ik}}{P_{jk}}$ : $P_{ik}$를 $P_{jk}$로 나눠준 값
- $w_i$ : 중심 단어 i의 임베딩 벡터
- $\tilde{w_k}$ : 주변 단어 k의 임베딩 벡터
이때 GloVe의 손실 함수는 다음과 같습니다.
$$J = \sum_{i, j=1}^V f(X_{ij})(w_{i}^T \tilde{w_j} + b_i + \tilde{b_j} - logX_{ij})^2$$
위 수식에서 우측의 괄호를 보면 중심 단어와 주변 단어 벡터의 내적이 동시 등장 빈도의 로그 값과의 차이를 줄이도록 설계되었음을 볼 수 있습니다.
그리고 손실 함수에서 $f(X_{ij})$ 함수는 가중치 함수(weighting function)로 동시 등장 빈도의 값 $X_{ij}$에 따라 가중치를 주기 위해 도입한 함수입니다.
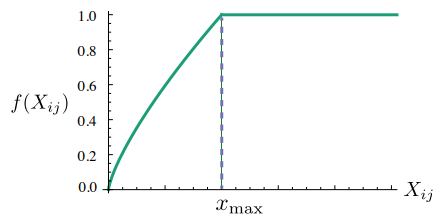
하지만 지나친 가중치를 주지 않기 위해 함수의 최댓값을 1로 설정했습니다.
https://brunch.co.kr/@learning/8
한국어를 위한 어휘 임베딩의 개발 -2-
한국어 자모의 FastText의 결합 | 이 글은 Subword-level Word Vector Representations for Korean (ACL 2018)을 다룹니다. 두 편에 걸친 포스팅에서는 이 프로젝트를 시작하게 된 계기, 배경, 개발 과정의 디테일을 다
brunch.co.kr
https://nlp.stanford.edu/pubs/glove.pdf
05) 글로브(GloVe)
글로브(Global Vectors for Word Representation, GloVe)는 카운트 기반과 예측 기반을 모두 사용하는 방법론으로 2014년에 미국 스탠포드대 ...
wikidocs.net
https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/06/pcasvdlsa/
SVD와 PCA, 그리고 잠재의미분석(LSA) · ratsgo's blog
이번 포스팅에서는 차원축소(dimension reduction) 기법으로 널리 쓰이고 있는 특이값분해(Singular Value Decomposion)와 주성분분석(Principal Component Analysis)에 대해 알아보도록 하겠습니다. 마지막으로는 이
ratsgo.github.io
'AI > NLP Study' 카테고리의 다른 글
| [NLP] BM25를 이용한 영화 추천 (0) | 2023.01.07 |
|---|---|
| [NLP] 임베딩 편향성 (0) | 2022.10.02 |
| [NLP] 텍스트 카테고리 분류 (1) | 2022.09.29 |
| [NLP] 텍스트 벡터화 (0) | 2022.09.27 |
| [NLP] 단어사전 만들기 (1) | 2022.09.25 |



